Earlier this week I was listening to an interesting lecture from the David & Inez Myers Professor in Computational Neuroscience at the Hebrew University of Jerusalem, Prof. Idan Segev. His lecture focused on exploring historical neuron models. Specifically, Prof. Segev was examining the McCulloch-Pitts model (MCP) for an artificial neuron and Wilfrid Rall’s model which includes classical cable theory for dendrites (the “Rall model”).
The McCulloch-Pitts model is an extremely simple artificial neuron model with inputs and outputs that could be either a zero or a one with each synaptic input being either excitatory or inhibitory. The dynamic of the MCP model was to simply sum the inputs. If an input is one, and is excitatory in nature, it added one. If it was one, and was inhibitory, it subtracted one from the sum. This is done for all inputs, and a final sum is calculated. The Rall model on the other hand, is a more complex model which incorporates certain spatial and temporal attributes that allow for a far more robust view of neuron mechanics.
While Prof. Segev’s walkthrough of the neuron models was fascinating–it was his emphasis on considering the utility of a model by its resolution or “granularity” that truly grabbed me. He explained that we should utilize whatever level of resolution is relevant, in terms of modeling, to maximize utility in an effort to understand the phenomena under investigation. While the opportunity to incorporate many details into our model may exist—we may only need a simplified abstraction to comprehend the mechanics of a phenomena.
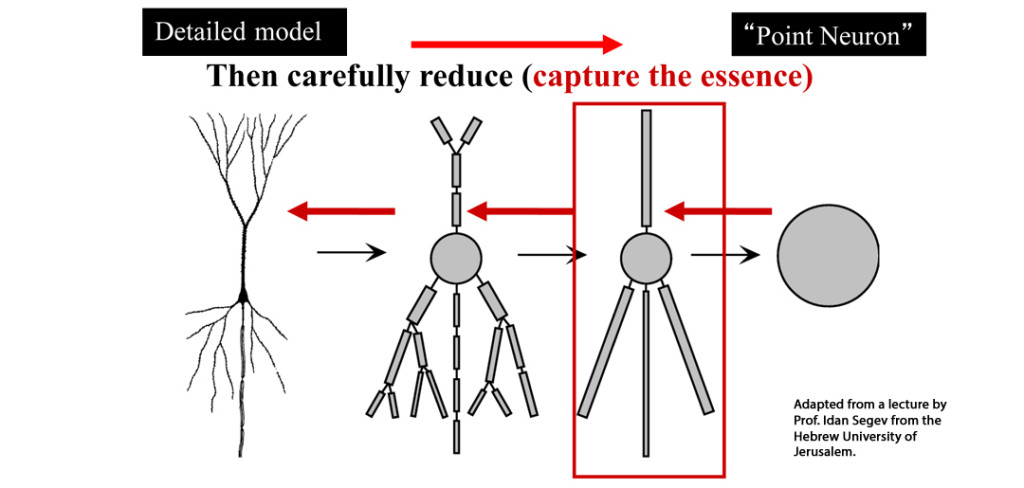
Interestingly enough, Prof. Segev went on to present two well-known sculptures to further solidify this point. He placed Rodin’s “The Kiss” next to Constantin Brancusi’s 1907-08 sculpture of the same title. He then explained that while Rodin’s kiss was indeed a more representational simulation of an actual kiss—the Brancusi piece was able to communicate the essence, or the abstract of the idea (a kiss), without numerous details that may cloud theory. It was a very interesting demonstration. 
This emphasis on model resolution really hit home for me as it is a concept I have been trying to communicate in regards to the Itten Color wheel and the Munsell Colors System for some time. The Itten Wheel (IW) is my “MCP” model. It is an abstract illustrative organization of “generic color” intended to illustrate simplified hue relationships. The wheel contains twelve hues: three primary, three secondary, and six intermediate colors. While the configuration of hues populating IW is not an accurate depiction of what many understand as “colorspace”, the adaptable abstract allows the observer to make reasonable predictions regarding the general behavior of available pigments.
The Munsell Color system, on the other hand, is a far more substantial color model. It consists of three independent dimensions which can be represented as an irregular, somewhat cylindrical, color solid: hue, measured by degrees around horizontal circles; chroma, measured radially outward from the neutral (gray) vertical axis; and value, measured vertically from 0 (black) to 10 (white). By incorporating these additional attributes of color, users can more accurately and consistently communicate specific colors and chart controlled courses through “colorspace.”
While I would not be one to argue the above mentioned benefits of the Munsell Color System, it is the compact abstraction of the Itten Wheel that provides me with the greatest utility for my painting endeavors. It can offer a relative frame of reference by which I can make informed decisions amidst either a pedantic or organic painting process. I can look to any color I am working with—and within the framework communicated by the IW–I can navigate with reasonable success.
So remember, next time you are preparing to effectively explore or navigate specific phenomena—Complexity does not always ensure maximal utility. Consider those devices that can hold the essence of a concept and still maximize utility.
Happy New Year and Happy Painting!